How Do Computers Add? Part 1
Have you ever wondered how computers and calculators—both of which are nothing more than mindless boxes of plastic, wires, and other strange parts—manage to add numbers? And so quickly! Math Dude has the answer.
Jason Marshall, PhD
Listen
How Do Computers Add? Part 1
Have you ever wondered how computers and calculators—both of which are nothing more than mindless boxes of plastic, wires, and other strange parts—manage to do something as intelligent as add numbers? And so quickly at that! How do they do it? And what does it have to do with the binary numbers and Boolean algebra we’ve been talking about lately? Stay tuned because those are exactly the questions we’ll be answering over the next few weeks..
Review: Boolean Algebra
For the past few weeks we’ve been trying to figure out how computers and calculators add. We started by talking about the binary number system, we then talked about some binary number tricks and how to perform binary addition, and then we talked about something called Boolean algebra. The first important thing to remember about Boolean algebra is that it’s a type of math that deals with bits instead of numbers like you’re used to. What’s a bit? It’s simply a binary digit, and it can be equal to 1 (aka, “true”) or 0 (aka, “false”), and nothing else.
See also: What’s the Difference Between 32-bit and 64-bit?
The second important thing to remember about Boolean algebra is its 3 fundamental operations: AND, OR, and NOT. What do they do? Well, NOT simply gives you back the opposite value of the bit you give it. So NOT 0 is equal to 1 and NOT 1 is equal to 0. AND and OR both take the values of two bits and give you back 1 or 0. AND gives you 1 back only if both input bits are equal to 1, and OR gives you 1 back if either (or both) input bits are equal to 1. Amazingly, these three operations—NOT, AND, and OR—are the keys to understanding how computers add.
Boolean Algebra and Sets
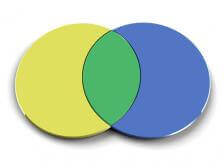
Before we talk about why these three operations in Boolean algebra are so important to computers, let’s take a minute to answer the questions I asked you to think about at the end of the last episode. I mentioned that you were probably already (unknowingly) familiar with Boolean algebra. To figure out what I meant by that, I encouraged you to go back and take a look at the Math Dude episodes on the union and intersection of sets and Venn diagrams. So, what’s the relationship between these things? Well, if you think about it, you’ll see that the union of two sets is the same as the OR operation in Boolean algebra. And the intersection of two sets is the same as the AND operation.
You can think of this in terms of a Venn diagram containing two partially overlapping circles that each represents the possible values of a single bit. The area inside of a circle represents the value of 1 for that bit and the area outside of a circle represents the value of 0. As we’ve learned in the episode on sets, the union of two sets is given by the combined area of both sets. In terms of Boolean algebra, the OR operation returns 1 for any pair of values located inside this combined region. On the other hand, the intersection of two sets is given by the shared area contained in both sets. If you think about it, you’ll see that this overlapping area is exactly the region in which the AND operation in Boolean algebra returns 1.
Logic Gates
So that’s how the math of Boolean algebra works, but what does all of this have to do with computers? The answer is amazing: We (by which I mean clever engineers) can actually design and build tiny physical electronic devices that implement these Boolean operations. These little devices are called “logic gates” and, analogous to the idealized mathematical versions we talked about, these physical devices have wires leading into them that signal the values of input bits (1 if the voltage on the wire is above some threshold and 0 otherwise) and a single wire leading out of them that gives the return value. By combining gates together in smart ways, they can be made to let you do incredible things like add numbers, write emails, play video games, chat with people around the world, and everything else you do with computing devices.
Since this isn’t a show about electrical engineering, we aren’t going to go into all the details of how you actually use wires, silicon, and a bunch of other stuff to build AND, OR, and NOT logic gates. Instead, we’re going to focus on this task of combining them together to do interesting mathematical things. But, unfortunately, we’re all out of time for today. So the ultimate answer to the burning question of how computers and calculators add—and the end of our quest to find it—will have to wait until next time.
Wrap Up
In the meantime, remember to become a fan of the Math Dude on Facebook where you’ll find lots of great math posted throughout the week. If you’re on Twitter, please follow me there, too. Finally, please send your math questions my way via Facebook, Twitter, or email at mathdude@quickanddirtytips.comcreate new email.
Until next time, this is Jason Marshall with The Math Dude’s Quick and Dirty Tips to Make Math Easier. Thanks for reading, math fans!
Venn Diagram image from Shutterstock
About the Author
Jason Marshall is the author of The Math Dude’s Quick and Dirty Guide to Algebra. He provides clear explanations of math terms and principles, and his simple tricks for solving basic algebra problems will have even the most math-phobic person looking forward to working out whatever math problem comes their way.