How Many Gifts Are in the 12 Days of Christmas?
How many gifts should one’s true love be given on each of the 12 Days of Christmas? If you stick to recommendations from the classic song, the answer can be calculated using some clever math. Keep on reading to find out how.

So Christmas was weird for me last year. It all started on December 25 when my true love gave me a potted pear tree upon whose branches sat a befuddled bird. Things got even weirder the following day when I received yet another pear tree (complete with yet another bird), as well as a pair of doves. The story on the third day was similar—another pear tree, two more doves, and this time a trio of chickens. As you might imagine, I was wondering: What’s up with all the birds?
This sort of thing continued for more than another week. With each new day came a new gift—actually a predictable number of that new gift: 3 on the 3rd day, 4 on the 4th, 5 on the 5th, and so on—as well as a repeat of all the gifts given on all of the previous days. By the time we got to the 12th day, we ran out of space in the castle living room and had to move our holiday celebration to the very dining room in which this painting is hanging.
That evening as we sat around the table, somebody asked me how many presents my true love had given on each day? With that question we began a quest to understand the mathematics of those epic twelve days of Christmas. To the best of my recollection, dear reader, the following contains an accurate recounting of that tale of discovery.
The Wonderful (and Distracting) World of Puzzles
As so often happens, our journey towards counting my true love’s gifts was quickly derailed by another math puzzle. Somebody at the table mentioned that someday far into the future (in the year 2016), psychologist and magician Richard Wiseman (who was once a guest on the famous “Math Dude” show) would tweet the following series of instructions (which you should feel free to follow along with … you might want to go grab a calculator):
- Type your house number (i.e., your address) into a calculator.
- Now double it.
- Next add 5 to the result.
- Then multiply this answer by 50.
- Now add your age.
- And then add 365 to the result.
- Finally, subtract 615 from the whole thing.
What do you get? As Wiseman points out: “Voila—your house number and age!” Needless to say, all of us at the table gave it a go, and much to our amazement we found that it does indeed work (so long as you’re less than 100 years old). Upon realizing this, roars of curiosity erupted: “Why? Huh? How can this be? I MUST KNOW NOW!”
So, exactly how does this puzzle from the future work? Good question, dear reader.
Alas, we don’t have time for an answer right now (and my space to write on the back of this painting is limited). So I’m going to let you think about it for a bit and see if you can come up with the answer yourself (but fear not, the answer will be revealed in a future Math Dude).
This is also what I told my guests for dinner that evening. So instead of allowing this to distract us from our true and noble goal, we dove back into our quest to understand the numbers behind my twelve days of gifts.
How Many Presents On Each Day?
On the first day of Christmas, my true love gave me one gift (the bird in a pear tree). On the second day of Christmas, my true love gave me 3 gifts (a pear tree and a couple of doves). On the third day of Christmas, my true love gave me 6 gifts (a pear tree, a couple of doves, and three chickens).
Upon thinking this through, my dinner companions and I wondered if there was a pattern here. One of us realized that if we used little dots to represent presents, then we could arrange the dots from each successive day’s presents into successively larger triangles.
In other words, the first day’s single present is a single dot. Then if we put two dots diagonally next to that single dot, we get a triangle with three total dots representing the three total presents from the second day. Adding three more dots in a diagonal line to this three-dot triangle gives us a six-dot triangle representing the total number of presents on the third day. And so on for each successive day—the number of dots in each triangle represents the number of presents for each day.
The number of dots that you obtain with each successive triangle (and thus the number of gifts received on each successive day) are known in mathematical circles as “triangular numbers” since they can be used to construct triangles.
The Gift of Triangular Numbers
The next question was could we come up with some way to quickly figure out how many dots—or rather gifts—I had received on each day without resorting to simply counting the dots? In other words, could we figure out a simple formula to calculate triangular numbers?
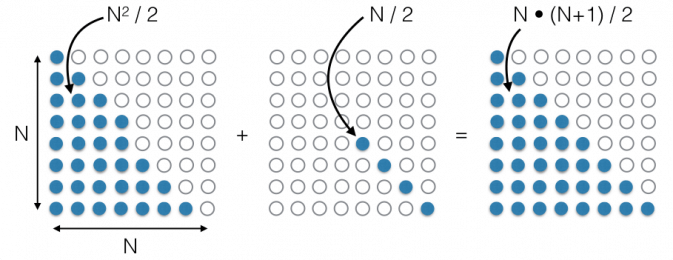
Sure enough, some clever person at the table (the name might have been Gauss) figured out that if you wanted to know the presents received on the Nth day of Christmas (where N could be 3, 4, 5, 12, or whatever), then you could calculate it quickly by thinking about a box made up of N by N dots. If you think about it, you’ll realize that the number of gifts on the Nth day is given by the number of dots in the triangle made up of all the dots below and including those on the diagonal of the N by N square.
What is this number? Well, there are N•N dots in a square (that’s the area of a square), so there must must be N•N/2 dots in half a square. But that isn’t quite the triangular number we’re after because it’s missing half the dots along the diagonal of the square. How many dots is that? It’s N/2 more dots. So the total number of dots in the triangle is actually: N•N/2 + N/2. Rearranging this a bit, my dinner companions and I found that the number of presents my true love gave me on the Nth day of Christmas must be:
Number of Gifts on Nth Day = N • (N+1) / 2
So, how many presents did I receive on the 5th day of Christmas? Our newly discovered handy-dandy formula says that it must have been 5•6/2 = 15. How about the 10th day? 10•11/2 = 55 presents. And the 12th day? 12•13/2 = 78 presents!
The Legend of the Twelve Days of Christmas
As I said at the outset, Christmas was a little weird for me last year. And now, dear reader, you know why. My true love went a bit overboard with gift-giving and things got a little out-of-hand in the castle. But despite all of the birds and the trees (not to mention the cows, drummers, and dancers), the best gift of all was the time spent with loved-ones around the table discovering beautiful secrets hidden in the world of math…
At least that’s what legend says the young girl and boy discovered on the back of that painting in their castle dining room all those years ago. In truth, nobody knows for sure because, sadly, that painting was lost to history. But, thankfully, the math, the puzzles, and the song recounting those epic “12 Days of Christmas” are still with us.
Or at least that’s the story of this song that I’ve decided to tell my daughter this year.
Wrap Up
Okay, that’s all the math we have time for today.
For more fun with math, please check out my book, The Math Dude’s Quick and Dirty Guide to Algebra. Also, remember to become a fan of The Math Dude on Facebook and to follow me on Twitter.
Until next time, this is Jason Marshall with The Math Dude’s Quick and Dirty Tips to Make Math Easier. Thanks for reading, math fans!
”Partridge in a pear tree” image from Shutterstock.