How to Think About Addition
What is addition? Of course you know the answer to this question, but do you really feel the answer—do you feel addition deep down in your gut?
In many ways mathematics begins with addition and subtraction. After all, the uniqueness of the infinity of numbers depends upon the fact that some separation exists between them—and we can use addition and subtraction to cross the separations from one to the next.
Everybody seeing this no doubt already gets addition and subtraction at some level. But do you really feel them? Hopefully you developed an intuitive feel for their meaning way back when you first learned to count. But I’m a firm believer that it never hurts to reinforce our intuition with even more intuition to ensure that we really do feel things way, way deep down within our gut. So that’s our plan for the next few weeks.
With that in mind, the question for today is: How should we think about addition so that we develop a good deep-down-in-the-gut feel for it? Let’s find out.
Addition With Integers
To kick things off, let’s start with a simple question: What is addition? There are no doubt a bunch of ways you can think about it, but for our purpose I’m going to say that addition is the process of combining things or groups of things into a single bigger group of things. You can think of it as taking two or more piles of rocks, dollars, pumpkins, imaginary friends, or whatever else and putting them all together into a bigger pile, like this:
So addition is piling things up. Yes, I know this seems kind of obvious—it is—but that’s exactly what addition is! But does this way of thinking about it always make sense? Does it still work when we’re adding up stuff other than integers—stuff like fractions, irrational numbers, or maybe even variables?
Addition With Fractions
For the most part, yes … it’s the same. Although as soon as you expand your numerical horizons and start throwing these other items into the mix, things do get a bit more complicated. For example, let’s think about fractions. Of course, the actual meaning of addition doesn’t change when we move from integers to fractions—we’re still making a new pile from two or more initial piles—it’s just the mechanics of doing this piling up that changes. To see what I mean, take a look at this:
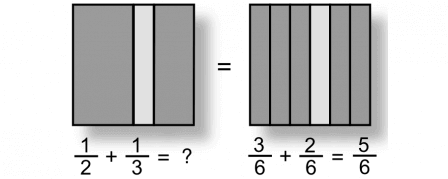
Suddenly, now that we’re dealing with fractions, it’s not so easy to add things up, is it? Sure, once you know how to do it, it’s not all that bad. But the picture is a bit different than when we were just dealing with positive integers making nice clean stacks of blocks. To see how to intuit the meaning of this slightly different form of pile-making, we can update our picture to look like this:
The trick is to find a way to rewrite 1/3 and 1/2 so that they both represent some number of the same type of somethings. In other words, we can’t straight-forwardly add 1/3 to 1/2 because they have different denominators—which means they represent different “types of somethings.” If we find a common denominator, we can express 1/3 and 1/2 in terms of some number of sixths. In particular, 1/3 = 2/6 and 1/2 = 3/6. Once they’re drawn this way, hopefully it becomes clear that we’re still just piling things up to make a new pile.
Addition With Variables
But what about adding variables into the mix—how does the meaning of addition change? The beautiful thing is that it doesn’t … it’s still the act of making a pile from several other piles. So once you know how to do addition with numbers, you know how to do it with variables, too.
For example, let’s say you need to come up with an expression that represents adding the number 5 to some as yet unknown quantity. Can we just do something like this:
Yep, sure can! What we’ve done here is to create a “something” called x which is represented by an x-box long stack of blocks. Of course, we don’t know the actual values of x, so we can imagine dotted lines midway along its stack representing the fact that we don’t really know how many total blocks there are. But the point is that we can still stick these two stacks together to make a bigger stack.
In other words, in this view, addition is still pictured as piling things up. That means that the expression we’re after for the sum is just x + 5. And it means that we can add a variable to a number in the exact same way that we add a number to another number.
Addition With Lots of Variables
Now let’s go bananas and imagine we need to come up with an expression that represents adding some variable to an entirely different variable. Just as we created a “something” called x before, we can now create a second “something” called y. The fact that we’ve given these variables different names means that they could have different values (we just don’t know what those values are yet). When we put them together, we get:
Again, we can stick the two stacks together to make a bigger stack—once again, we’re just making a single pile from two existing piles. And that means the expression we’re after for the sum is simply x + y. So, not only can we add numbers to variables, we can also add variables to other variables in the exact same way. But why stop at adding two things together. You can add any number of variables together just like you can add any number of numbers together:
Again, everything works as expected.
Wrap Up
The key thing to realize is that in each of these cases—integers, fractions, or variables—we’re doing the same thing … we’re piling things up, or stacking things up, or whatever else you want to call it. That’s addition. It’s as simple as can be. But it’s also as important as can be. And it’s something that any math fan should feel in their gut. Do you?
Okay, that’s all the math we have time for today. For more fun with math, please check out my book, The Math Dude’s Quick and Dirty Guide to Algebra. Also, remember to become a fan of The Math Dude on Facebook and to follow me on Twitter.
Until next time, this is Jason Marshall with The Math Dude’s Quick and Dirty Tips to Make Math Easier. Thanks for reading, math fans!
Addition image courtesy of Shutterstock.
You May Also Like…
About the Author
Jason Marshall is the author of The Math Dude’s Quick and Dirty Guide to Algebra. He provides clear explanations of math terms and principles, and his simple tricks for solving basic algebra problems will have even the most math-phobic person looking forward to working out whatever math problem comes their way.
