Polygon Puzzle: How Many Degrees Are in a Polygon?
How many degrees are in the interior angles of a pentagon? A hexagon? An octagon? Or any polygon? Keep on reading The Math Dude to learn how to solve this polygon puzzle!
We recently talked about why the three interior angles of a triangle must always add up to 180º. And at various points in the past, we’ve noted that the quartet of 90º “right” angles in a square must mean that the interior angles of a square add up to 360º. But we’ve never talked about what happens when we toss more sides into the mix.
In other words, we’ve never talked about how to figure out the total number of degrees in a pentagon. Or a hexagon…or an octagon. Or any other polygon, for that matter! And just as importantly, we’ve never dealt with whether or not there’s some clever way to figure all of this out without resorting to making measurements with a protractor.
Until now, that is – because these are exactly the questions we’ll be talking about today as we dive into a delectably delicious polygon puzzler.
Sponsor: Visit GoDaddy.com to get your $2.95 .COM domain. Some limitations apply, see website for details.
Review: Interior Angles of Polygons
Our big goal for today is to figure out exactly how the interior angles of polygons change as the number of sides in the shape increases.
As a super quick review, a polygon is any shape made up of three or more connecting sides that you can draw on a flat sheet of paper. For a more thorough look at the definition of a polygon, check out the episode on that topic.
The angles formed in the interior of a polygon where pairs of sides intersect are called “interior angles.” As noted earlier, we’ve talked about using a clever trick to prove that a triangle’s interior angles always add up to 180º. And we’ve seen that the four right interior angles of a square (or any rectangle) must add up to 360º.
Which might lead you to wonder…
How Many Degrees Are In a Pentagon?
What happens when the number of sides increases beyond four? In other words, what’s the sum of the interior angles of a pentagon, a hexagon, an octagon, or any other polygon?
Interior angles get larger as the number of sides increases.
Let’s start by taking a look at the 5-sided regular polygon (meaning, its sides and angles are all equally sized), better known as a pentagon. If you sketch a pentagon, you’ll immediately see that its interior angles are all greater than 90º. So the first thing we can conclude is that the interior angles of a polygon get larger as the number of sides increases. But by how much?
At this point, I encourage you to stop for a minute and see if you can figure out how you might go about answering this question. If you’re having trouble getting started, think about the fact that you can draw a diagonal line across a 360º square to break it up into a pair of 180º triangles.
Hmm, very interesting. Now take a minute or two and see what you can come up with.
Any ideas yet?…
Isn’t this fun?…
OK, ready for the answer?…
Hopefully, you noticed that a 5-sided regular pentagon can be broken up into three triangles. To see this, draw a line from the top corner of your pentagon down to each of its opposing lower corners. Once you draw this picture, you’ll see that a pentagon is indeed composed of three triangles. And from that you should see that a pentagon must contain 3 x 180º = 540º.
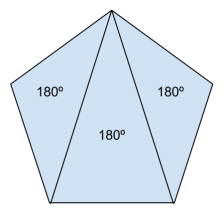
So if the interior angles of a 3-sided triangle add up to 180º, those of a 4-sided square add up to 360º, and those of a 5-sided pentagon add up to 540º. It looks like we keep adding 180º for each additional side. Does this trend hold up as we move to polygons with more and more sides?
How Many Degrees In a Hexagon, Octagon, Or Any Polygon?
To see, let’s make the next logical leap and move from thinking about a 5-sided pentagon to a 6-sided hexagon. Again, I encourage you to take a few minutes to think about what we’ve done so far, and see if you can puzzle out the total number of degrees contained in the interior angles of a hexagon.
Do you see the trick?…
Same idea as before…
Got it?…
To answer this question, draw yourself a lovely regular hexagon, and then draw three lines from one of its corners to the three opposing corners. When you do this, you should see that a hexagon can be broken up into four triangles. And, therefore, you should see that a hexagon must contain 4 x 180º = 720º.
Do you see a trend yet? If you really wanted to, you could continue this game for the 7-sided heptagon, the 8-sided octagon, and so on. In fact, you can do it for any and every polygon.
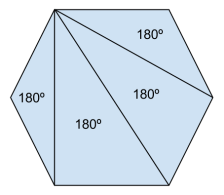
When you do that, you’ll find that an n-sided polygon (where n simply represents the number of sides in the polygon) can be broken down into n–2 triangles. Which means that the interior angles of an n-sided polygon will always add up to (n – 2) x 180º.
Which, lo and behold, is the answer to today’s great polygon puzzler!
Wrap Up
OK, that’s all the math we have time for today.
For more fun with math, please check out my book, The Math Dude’s Quick and Dirty Guide to Algebra. And remember to become a fan of The Math Dude on Facebook, where you’ll find lots of great math posted throughout the week. If you’re on Twitter, please follow me there, too.
Until next time, this is Jason Marshall with The Math Dude’s Quick and Dirty Tips to Make Math Easier. Thanks for reading, math fans!
Soccer ball image courtesy of Shutterstock.
You May Also Like…
About the Author
Jason Marshall is the author of The Math Dude’s Quick and Dirty Guide to Algebra. He provides clear explanations of math terms and principles, and his simple tricks for solving basic algebra problems will have even the most math-phobic person looking forward to working out whatever math problem comes their way.
