What Is a Great Circle?
Have you ever heard of a great circle? How about a small circle? Do the lines of longitude on Earth form great circles? How about the lines of latitude? How do these ideas explain the routes that airplanes fly? Keep on reading to find out!
Have you ever been on a flight, grabbed the magazine out of the seat-back pocket in front of you, and stumbled upon the page that shows the routes that airplanes take when flying hither and thither?
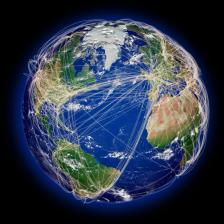
Were you surprised by what you saw? I know I was the first time I saw it…because the lines showing the flight paths between various cities around the globe are not straight!
Instead, these flight paths follow what appear to be crazy looping arcs. As it turns out, these arcs aren’t crazy at all—they’re called great circles, and they really are pretty great. What are they? And why do airplanes fly along them? Stay tuned because those are exactly the questions we’ll be answering today.
Sponsor: Want to save more, invest for the future, but don’t have time to be a full-on investor? Betterment.com helps you build a customized, low-cost portfolio that suits your goals. Learn more.
As the Airplane Flies
In the last episode, I left you to think about the fact that the fastest way to fly from Florida to the Philippines (which, mind you, is at a more southern latitude than Florida) is to actually take a path that goes way up north over Alaska! I know that sounds completely crazy-mad-nuts and totally counterintuitive, but it’s true.
My first experience with this sort of thing came years ago as I took a flight from Los Angeles to London. Sometime in the middle of the flight (which was also the middle of the night, so I was already a bit out of it), I remember looking out the window and seeing shiny white stuff way, way down below me extending as far as I could see. It took me a few minutes to realize it was sheets of ice…and that we were really far north—far enough that we eventually passed over the tip of Greenland.
Why do flights from Los Angeles to London, Orlando to Manilla, and any place else to anywhere else follow such seemingly strange routes? Would you believe me if I told you it’s because these crazy looking curved routes are actually the shortest distance between these cities? That they’re the analog of a straight line on a sphere? Whether or not you want to believe me, it’s true—let’s see why.
Great and Small Circles
To understand these flight paths, you need to know about great and small circles on Earth. To see what these are, let’s think about the route between Los Angeles and Atlanta. Why these two cities? Because they’re at nearly the same latitude (which means they’re both at approximately the same angular distance north of the equator). If I was to ask you to draw the shortest line between these two cities on a regular flat paper map, you’d likely draw an approximately horizontal line in the east-west direction connecting them. But that isn’t actually the shortest path.
The intersection of a random plane and a sphere will usually form a small circle.
Imagine taking a perfectly flat, rigid, and gigantic sheet of paper (it’s gotta be bigger than the Earth) and using it to slice the planet into two pieces along a line running around the globe parallel to the equator and passing through both Los Angeles and Atlanta. The path of intersection of this giant plane and the Earth creates a line that runs east-west around the globe in a circle and connects the two cities. This line is what’s called a small circle.
The intersection of a random plane and a sphere will usually form a small circle. But occasionally, this intersection instead forms a great circle. What’s that? Well, if in addition to passing through the two points on the surface of the Earth (in our case Los Angeles and Atlanta), the plane also passes through the Earth’s center, the resulting intersection is dubbed a great circle. And it turns out these great circles have a very important property.
Latitude and Longitude
But before we get to that mighty important property, let’s take a minute to think about the lines of latitude and longitude on the Earth. As you may know (but probably find it really hard to remember), lines of constant longitude run north-south between Earth’s two poles, and lines of constant latitude run in an east-west direction around the planet. I keep the two straight in my head by remembering that the word “lateral” implies some kind of sideways movement, which is the same direction that the lines of latitude run.
Given what we’ve learned about small and great circles, do the lines of longitude form small or great circles around the planet? If you think about it, you’ll see that circles formed by lines of longitude are always centered on the exact center of the Earth. Which means that these circles are great circles. How about lines of latitude? These east-west running circles are always centered at some point along Earth’s rotation axis, but not necessarily its center. So, with one exception, lines of latitude are examples of small circles. What’s the exception? I’m going to let you try to work that out on your own.
The Shortest Distance on a Sphere
As I mentioned earlier, great circles have a very important property. And that is that the shortest distance between two points on the surface of a sphere is always along the great circle connecting those points. In other words, if you take a piece of string and pull it taught between any two points on a model of the globe, that string will always represent the shortest distance between those points on the surface of the sphere. And the path that the string takes always lies along the great circle connecting those two points.
Will that always be the path that airplanes fly? Mostly, but not exactly. While geometry would say that the great circle path is always best, physics sometimes gets in the way. In particular, airplanes usually follow paths that differ slightly from great circles in order to take advantage of jet streams and get you where you’re going even faster. This little detail aside, when it comes to getting places quickly on the surface of a sphere, great circles rule the skies (and the seas, too). And they’re yet another beautiful example of the weird and wonderful world of non-Euclidean geometry.
Wrap Up
OK, that’s all the math we have time for today.
Please be sure to check out my book, The Math Dude’s Quick and Dirty Guide to Algebra. And remember to become a fan of The Math Dude on Facebook, where you’ll find lots of great math posted throughout the week. If you’re on Twitter, please follow me there, too.
Until next time, this is Jason Marshall with The Math Dude’s Quick and Dirty Tips to Make Math Easier. Thanks for reading, math fans!
Flight paths around Earth image courtesy of Shutterstock. Images of the ORL to MNL and LAX to LHR flight paths are from v-flyer.com.
You May Also Like…
About the Author
Jason Marshall is the author of The Math Dude’s Quick and Dirty Guide to Algebra. He provides clear explanations of math terms and principles, and his simple tricks for solving basic algebra problems will have even the most math-phobic person looking forward to working out whatever math problem comes their way.
